Articles
- Page Path
- HOME > J Prev Med Public Health > Volume 46(2); 2013 > Article
-
Original Article
Improving the Performance of Risk-adjusted Mortality Modeling for Colorectal Cancer Surgery by Combining Claims Data and Clinical Data - Won Mo Jang1, Jae-Hyun Park2, Jong-Hyock Park3, Jae Hwan Oh4, Yoon Kim5,6
-
Journal of Preventive Medicine and Public Health 2013;46(2):74-81.
DOI: https://doi.org/10.3961/jpmph.2013.46.2.74
Published online: March 28, 2013
1People's Health Institution, Seoul, Korea.
2Department of Social and Preventive Medicine, Sungkyunkwan University, Suwon, Korea.
3Division of Cancer Policy and Management, National Cancer Control Research Institute, National Cancer Center, Goyang, Korea.
4Center for Colorectal Cancer, National Cancer Center, Goyang, Korea.
5Institute of Health Policy and Management, Medical Research Center, Seoul National University, Seoul, Korea.
6Department of Health Policy and Management, Seoul National University College of Medicine, Seoul, Korea.
- Corresponding author: Yoon Kim, MD, PhD. 103 Daehak-ro, Jongno-gu 110-799, Seoul, Korea. Tel: +82-2-740-8362, Fax: +82-2-743-2009, yoonkim@snu.ac.kr
Copyright © 2013 The Korean Society for Preventive Medicine
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
-
Objectives
- The objective of this study was to evaluate the performance of risk-adjusted mortality models for colorectal cancer surgery.
-
Methods
- We investigated patients (n=652) who had undergone colorectal cancer surgery (colectomy, colectomy of the rectum and sigmoid colon, total colectomy, total proctectomy) at five teaching hospitals during 2008. Mortality was defined as 30-day or in-hospital surgical mortality. Risk-adjusted mortality models were constructed using claims data (basic model) with the addition of TNM staging (TNM model), physiological data (physiological model), surgical data (surgical model), or all clinical data (composite model). Multiple logistic regression analysis was performed to develop the risk-adjustment models. To compare the performance of the models, both c-statistics using Hanley-McNeil pair-wise testing and the ratio of the observed to the expected mortality within quartiles of mortality risk were evaluated to assess the abilities of discrimination and calibration.
-
Results
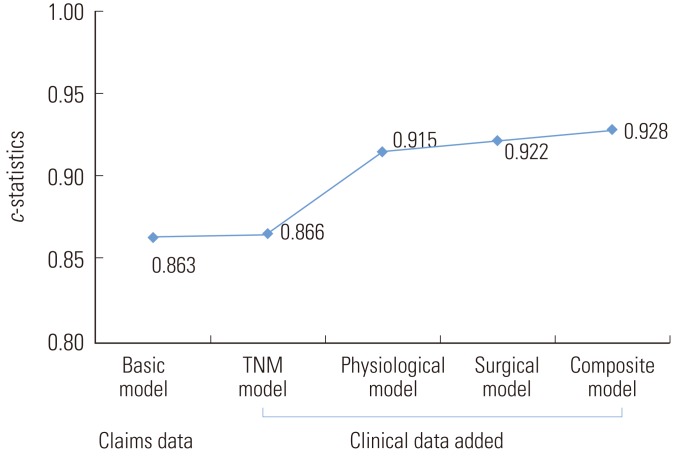
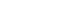
- The physiological model (c=0.92), surgical model (c=0.92), and composite model (c=0.93) displayed a similar improvement in discrimination, whereas the TNM model (c=0.87) displayed little improvement over the basic model (c=0.86). The discriminatory power of the models did not differ by the Hanley-McNeil test (p>0.05). Within each quartile of mortality, the composite and surgical models displayed an expected mortality ratio close to 1.
-
Conclusions
- The addition of clinical data to claims data efficiently enhances the performance of the risk-adjusted postoperative mortality models in colorectal cancer surgery. We recommended that the performance of models should be evaluated through both discrimination and calibration.
- Measuring the quality of healthcare services facilitates decisions about the selection of providers, the creation of financial incentives, and quality improvement for consumers, purchasers, and providers. There is an increasing demand for precise comparative information about service quality. In this regard, risk-adjustment methods are frequently used for the evaluation of the quality of patient outcomes [1,2]. Risk-adjustment data are typically derived from claims data and clinical sources [3]. Claims data have the advantages of ready availability, low cost, and large volume. These advantages warrant the use of claims data for risk-adjustment [3,4].
- In contrast, clinical data are more informative with regard to a patient's pathophysiological risk of death, rendering clinical data more accurate than claims data and a more popular basis for the evaluation of quality [3-8]. Some investigators have suggested an alternative approach to the use of data sources in risk adjustment: combining clinical data and claims data can overcome any disadvantages of one or the other and strengthen the advantages of both data sources [9,10].
- To date, studies combining claims and clinical data have focused only on cardiovascular disease [4,8,11]. Although cancer is the most common cause of mortality in South Korea, a lack of evidence exists comparing the performance of risk-adjustment cancer-mortality models based on data sources [7,12-14]. Furthermore, the discriminatory power of various models has not been evaluated by a probability method (e.g., pair-wise test) in numerous studies. Many comparative studies measuring the performance of risk-adjustment models are based on discrimination alone, not with calibration simultaneously, which can lead to avoidable controversy [1,3,4,6-9,11].
- Colorectal cancer had the third highest age-adjusted incidence (36.9 per 10 000 population) and was the fourth highest cause of age-adjusted mortality (12.0 per 10 000 population) in South Korea in 2011 [15]. Colorectal cancer was increasing in incidence relative to other types of cancer and as a cause of mortality in both men and women from 1999 to 2007 in South Korea [16]. The recent increase in the colorectal cancer incidence and mortality in South Korea means that measuring the quality of colorectal cancer surgery is of extreme importance. The purpose of this study was to improve the performance of risk-adjusted mortality models for colorectal cancer by combining claims and clinical data. Additionally, we attempted to compare both the discrimination and calibration performance of the models.
INTRODUCTION
- Data Sources
- The study sample consisted of patients who had undergone colorectal cancer surgery (colectomy, colectomy of the rectum and sigmoid colon, total colectomy, and total proctectomy) at five teaching hospitals in the Seoul metropolitan area during 2008. A total of 652 patients were treated who had a principal diagnosis of colorectal cancer according to the International Classification of Disease 10 code (C180-C189, C190, C200, D010-D019, and D099) and procedure codes identified by the Korean National Health Insurance billing system (Q1261, Q1262, Q2671, Q2672, Q2673, Q2679, QA671, QA672, QA673, QA679, Q2921, Q2922, Q2923, Q2924, QA921, QA922, QA923, QA924, Q2925, Q2926, QA925, and QA926). The sample size for comparison of the discriminatory power of the models was calculated with the assumption that type I error =0.05 and type II error =0.2. The mean discriminatory power of the claims data models (c=0.739) and clinical data models (c=0.881) in previous studies were applied [1,3-8,11,17,18]. Based on a pilot study, it was assumed that the Pearson correlation coefficient between the mortality probabilities of the two types of models was 0.8 [19] and that the ratio of the number of cases of survival to deaths was 27.3.
- Measures of Outcome and Prognostic Factors
- The outcome was defined as death occurring within 30 days of an operative procedure, either in the hospital or after discharge from the hospital, regardless of the cause [20,21]. From the claims data, we extracted prognostic factors including age, sex, health insurance, associated surgery, admission through the emergency room, lymph node dissection, and comorbidities (diabetes mellitus, hypertension, liver disease, other cardiac arrhythmia, and secondary cancer). Clinical prognostic factors were selected from the medical records by a full-time nurse reviewer who was trained in data extraction and included TNM staging, history of past surgery, emergency surgery, body mass index, serum albumin levels, the American Society of Anesthesiologists (ASA) score, and perforation and obstruction of the colon. The prognostic factors were selected by three faculty members who practiced colorectal cancer surgery in academic teaching hospitals through a review of previous literature and exploratory statistical results [7,12-14,20-29]. Meetings for the selection of prognostic factors were held four times, selection of claims data and clinical data and a review of the results of the models were performed. Dividing the value of the variables was also based on clinical judgment.
- Study Design and Statistical Analysis
- To compare the performance of models according to their data sources, five models were constructed using candidate prognostic factors. The basic model used standard claims data including age, sex, health insurance, associated surgery, admission through the emergency room, lymph node dissection, and comorbidities. The TNM model used claims data plus TNM staging. The physiological model used claims data plus the ASA score, serum albumin levels, and body mass index. The surgical model used claims data plus emergency surgery, TNM staging, past surgery history, perforation of the colon, and obstruction of the colon. The composite model used claims data plus all the clinical data.
- To avoid the use of secondary diagnoses that develop during hospital stays as prognostic factors, we used only the secondary diagnoses that occurred during the 12 months prior to the first admission. We used multiple logistic regression to develop models and bootstrapped entire data sets by repeating the steps 1000 times to prevent overfitting [30-32].
- We examined the performance of the models according to two criteria: discrimination and calibration [33]. The discriminatory power of the models was evaluated using c-statistics, or areas under the receiver operating characteristic curve, according to Hanley-McNeil pair-wise tests [34]. The goodness of fit of each model was evaluated using Hosmer-Lemeshow statistics. To compare the power of calibration among the models, we first created log-log scatter plots of the models compared with top-flight discrimination models and calculated the observed/expected (O/E) ratios and 95% confidence intervals within each quartile of mortality for each of the models [3]. The quartiles represented four categories of estimated mortality risk. Subgroup analyses were performed by comparing the observed and expected 30 day postoperative mortality according to age, TNM staging, ASA score, and obstruction of the colon [20].
- This study was approved by the institutional review board of the Seoul National University College of Medicine. All statistical analyses were performed using SAS version 9.1 (SAS Institute, Cary, NC, USA).
METHODS
- Of the total sample (n=652), 3.5% of patients died (n=23). The mean age was 64.2 years, and more than 62.5% of the patients were male. The distribution of surviving persons differed by age, secondary cancer, admission through the emergency room, lymph node dissection, emergency surgery, TNM staging, body mass index, ASA score, perforation of the colon, and obstruction of the colon (Table 1). The odds ratios of the prognostic factors by model are shown in Table 2. The odds ratios of other cardiac arrhythmia, secondary cancer, admission through the emergency room, perforation, and ASA score had p-values less than 0.05.
- Figure 1 presents the c-statistics for each risk-adjustment model, showing that the physiological model (c=0.915), surgical model (c=0.922), and composite model (c=0.928) had impressive results. These three models displayed similar levels of improvement in discrimination, whereas the TNM model (c=0.87) was only slightly better than the basic model (c=0.86). The discriminatory power did not differ among the developed models (p>0.05) based on the paired comparison of c-statistics of the models using the Hanley-McNeil test.
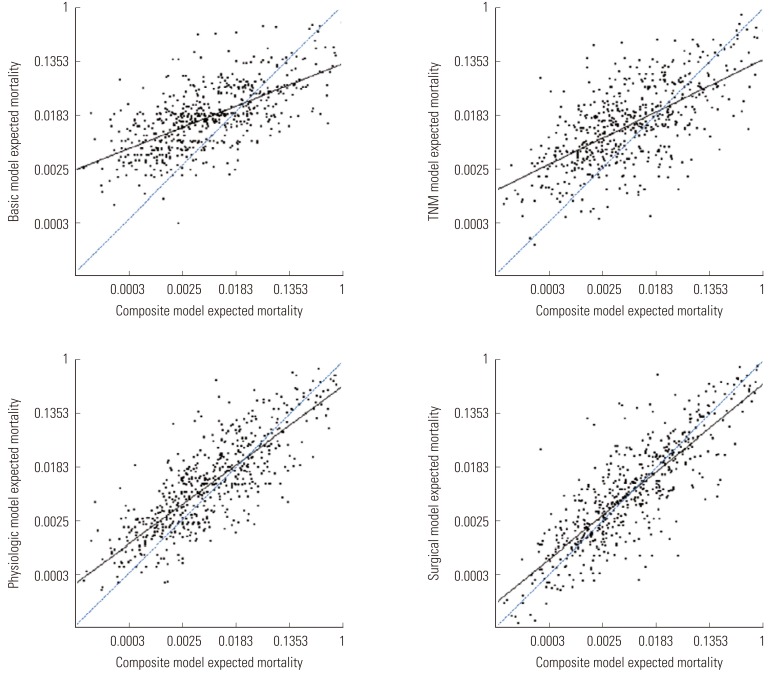
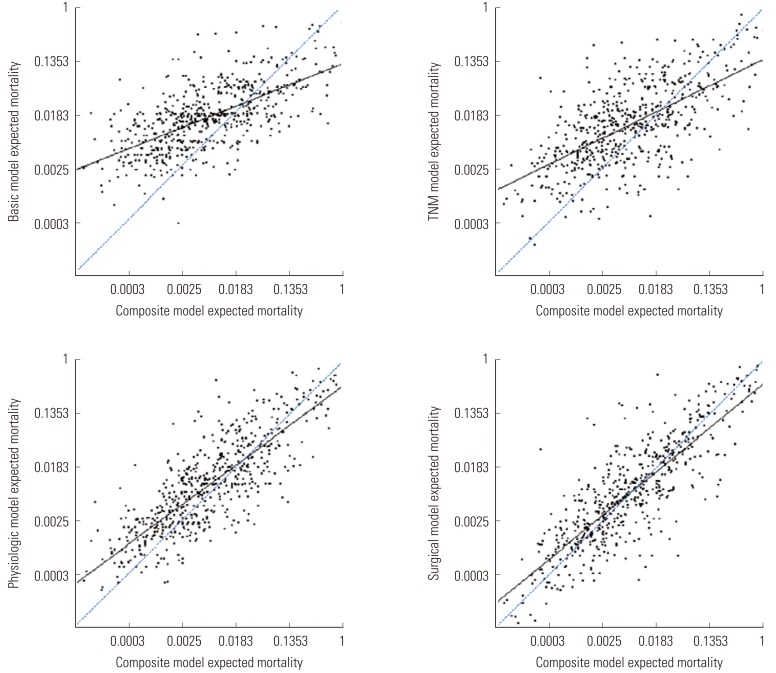
- The data on mortality generated by the basic, TNM, physiological, and surgical models showed greater clustering among moderate-risk patients and greater variability among the lower- and higher-risk patients compared with the composite model (Figure 2). The surgical model and physiological model were more similar to the composite model in terms of the expected mortality than were the basic and TNM models. This was reflected in the degree of difference between the fitted and reference lines, which means the calibration abilities compared to the composite model (slope=1).
- Table 3 shows the O/E ratios of the five models by quartiles based on the expected mortality. In the lower-risk quartiles (quartiles A & B), all models overestimated the mortality risk (O/E ratio <1), whereas most models underestimated mortality in the higher-risk quartiles (quartiles C & D) (O/E ratio >1). Overall, the composite and surgical models displayed O/E ratios closer to 1 than did the other models. In quartile A, the composite model displayed an O/E ratio closest to 1, and the surgical model showed the next closest estimate. In quartile B, the TNM model displayed an O/E ratio closest to 1, with the basic model providing the next closest estimate. In quartile C, the surgical model displayed an O/E ratio closest to 1, and the composite model had the next closest value. In quartile D, the composite model displayed an O/E ratio closest to 1, with the surgical model displaying the next closest value. The subgroup analyses revealed that the expected mortality by age, TNM staging, ASA score, and obstruction of the colon was well within the 95% confidence limits of the observed outcome and did not differ among the subgroups.
RESULTS
- The level of model discrimination in this study (c=0.863-0.928) was relatively higher than the models examined in previous risk-adjustment studies of colorectal cancer mortality (c=0.707-0.848) [20,21,28]. This was evident in the claims-data models as well as in the model using a combination of claims data and clinical data. The level of model discrimination in this study may be effective because more relevant postoperative complication factors (physiologic factors and surgical factors) were selected. We used a minimum of 13 prognostic factors and a maximum of 19 to construct the risk-adjusted models. In previous studies, 4 to 13 factors have been used. We speculated that the relevance of the prognostic factors for mortality, rather than the number of prognostic factors, affected the discriminatory power of the models. According to studies by Steyerberg et al. [35], c-statistic levels are not necessarily proportional to the number of prognostic factors. Even with a large number of prognostic factors, the possibility of a low discriminatory power exists. In small data sets, the likelihood of this possibility increases.
- Although the addition of the TNM staging data alone to the claims data resulted in only marginal improvement in discriminatory power, the addition of further clinical data led to remarkable improvements. The extent of cancer spread reflected in TNM staging may predict long-term outcomes (5-year or 10-year survival) more strongly than short-term outcomes (30-day or in-hospital operative mortality) [36,37]. However, physiological parameters, emergency surgery, and obstruction and perforation of the colon were important predictors of the short-term outcome [12,37,38]. In previous studies, the ASA score was used as a proxy for physiological condition [20,38].
- Beyond the quality of surgery (i.e., completeness of resection, adequacy of nodal examination, utilization of adjuvant treatments, aggressiveness of postresection cancer follow up), multiple factors including anesthesia care, preoperative evaluation, nurse staffing and training, intensive care unit management and staffing, 24-hour in-house resident or physician coverage, and emergency response can affect the short-term outcome of cancer surgery [36]. Further studies are required to evaluate the performance of risk-adjusted long-term mortality models. Although the c-statistics for these models were not statistically different, subtle differences were evident, suggesting that a larger sample size may lead to more apparent differences.
- The enhancement of the discriminatory power declined with the addition of clinical data to the claims data. The saturation of discriminatory power reflected in our results was similar to the findings of previous studies [4,9]. Pine and colleagues showed that the performance of the claims data model was enhanced by the addition of presentation on admission (POA) codes and limited laboratory data [4]. However, the addition of POA codes resulted in the greatest improvement in discrimination, and this enhancement declined with the addition of other factors. Fry and colleagues additionally showed that saturation in discrimination was provided by POA codes with the addition of numerical laboratory data [9]. According to Hall et al. [3], the cost per patient to obtain key clinical findings from the medical charts was 50 dollars in 2007; this cost must be balanced against the minimal enhancement of model performance derived from the collection of these data.
- To select a model for the evaluation of quality of care, it is necessary to examine the levels of both discrimination and calibration. It is important to select precise risk-adjustment models when measuring quality, but testing discrimination alone is insufficient. It is difficult to differentiate the discriminatory power of models despite thorough pair-wise testing, and it would therefore be useful to select a suitable model by testing the calibration through the log-log scatter or O/E ratio. Our results demonstrated little statistical difference in the discriminatory power of the models examined here. The absolute levels differed only slightly among the physiological, surgical, and composite models, but were clearly differentiated by the calibration of the models. Our models appeared to overestimate mortality in the low-risk patients and to underestimate mortality among high-risk patients. This was similar to the results of Hall et al. [3], and careful research efforts are needed to identify the reasons for these biases.
- There were several limitations of this study. First, the confidence intervals were greater than 10, which had p-values of the odd ratios of prognostic factors of less than 0.05. This may have been dependent on the limited sample size of deaths (23 of 652). Second, we used non-sequential data from five volunteer institutions. This can limit generalization to other populations. Third, we constructed parsimonious risk-adjustment models for colorectal cancer only. The prognostic factors were specific only to colorectal cancer surgery, which makes them inappropriate for application to other forms of cancer surgery. Third, we only considered secondary diagnoses that occurred during the 12 months prior to initial admission. We have not yet evaluated our approach to the definition of secondary diagnoses relative to previous POA coding algorithms such as those applied in New York and California. Fourth, a more extensive systematic training program on clinical data extraction is needed to perform precise extraction of variables from clinical records in South Korea.
- In summary, our data suggest that the addition of clinical data to claims data could efficiently enhance the performance of risk-adjusted postoperative mortality models of colorectal cancer surgery. The addition of TNM data could contribute to improved performance in combination with other surgical data including the ASA score and emergency surgery. We additionally recommend that the performance of risk-adjustment models should be evaluated based on both discrimination and calibration. Testing only discrimination may result in an insufficient comparison of the performance of risk-adjustment models.
DISCUSSION
- 1. Steinberg SM, Popa MR, Michalek JA, Bethel MJ, Ellison EC. Comparison of risk adjustment methodologies in surgical quality improvement. Surgery 2008;144(4):662-667. 18847652ArticlePubMed
- 2. Lindenauer PK, Remus D, Roman S, Rothberg MB, Benjamin EM, Ma A, et al. Public reporting and pay for performance in hospital quality improvement. N Engl J Med 2007;356(5):486-496. 17259444ArticlePubMed
- 3. Hall BL, Hirbe M, Waterman B, Boslaugh S, Dunagan WC. Comparison of mortality risk adjustment using a clinical data algorithm (American College of Surgeons National Surgical Quality Improvement Program) and an administrative data algorithm (Solucient) at the case level within a single institution. J Am Coll Surg 2007;205(6):767-777. 18035260ArticlePubMed
- 4. Pine M, Jordan HS, Elixhauser A, Fry DE, Hoaglin DC, Jones B, et al. Enhancement of claims data to improve risk adjustment of hospital mortality. JAMA 2007;297(1):71-76. 17200477ArticlePubMed
- 5. Shahian DM, Silverstein T, Lovett AF, Wolf RE, Normand SL. Comparison of clinical and administrative data sources for hospital coronary artery bypass graft surgery report cards. Circulation 2007;115(12):1518-1527. 17353447ArticlePubMed
- 6. Gordon HS, Johnson ML, Wray NP, Petersen NJ, Henderson WG, Khuri SF, et al. Mortality after noncardiac surgery: prediction from administrative versus clinical data. Med Care 2005;43(2):159-167. 15655429ArticlePubMed
- 7. Park HK, Yoon SJ, Ahn HS, Ahn LS, Seo HJ, Lee SI, et al. Comparison of risk-adjustment models using administrative or clinical data for outcome prediction in patients after myocardial infarction or coronary bypass surgery in Korea. Int J Clin Pract 2007;61(7):1086-1090. 17537190ArticlePubMed
- 8. Scott IA, Thomson PL, Narasimhan S. Comparing risk-prediction methods using administrative or clinical data in assessing excess in-hospital mortality in patients with acute myocardial infarction. Med J Aust 2008;188(6):332-336. 18341455ArticlePubMedPDF
- 9. Fry DE, Pine M, Jordan HS, Elixhauser A, Hoaglin DC, Jones B, et al. Combining administrative and clinical data to stratify surgical risk. Ann Surg 2007;246(5):875-885. 17968182ArticlePubMed
- 10. Pine M, Norusis M, Jones B, Rosenthal GE. Predictions of hospital mortality rates: a comparison of data sources. Ann Intern Med 1997;126(5):347-354. 9054278ArticlePubMed
- 11. Geraci JM, Johnson ML, Gordon HS, Petersen NJ, Shroyer AL, Grover FL, et al. Mortality after cardiac bypass surgery: prediction from administrative versus clinical data. Med Care 2005;43(2):149-158. 15655428ArticlePubMed
- 12. Kang DB, Shin CY, Lee JK, Park WC. Multivariate analysis of the risk factors associated with complications and mortality after and emergency operation for obstructive, perforated colorectal cancer. J Korean Soc Coloproctol 2009;25(3):165-171. (Korean)Article
- 13. Lee HJ, Oh JH, Lee JN, Baek JH, Chung M, Lee WK, et al. Prognostic factors associated with surgical mortality conferred by emergency operation in colorectal cancer. J Korean Soc Coloproctol 2006;22(5):301-307. (Korean)
- 14. Park YJ, Park KJ, Park JG, Lee KU, Choe KJ, Kim JP. Prognostic factors in 2230 Korean colorectal cancer patients: analysis of consecutively operated cases. World J Surg 1999;23(7):721-726. 10390594ArticlePubMed
- 15. National Cancer Information Center. Incidence and mortality of cancer. 2012. cited 2012 Dec 28. Available from: http://www.cancer.go.kr/ncic/cics_f/01/011/index.html. (Korean)
- 16. Ministry of Health and Welfare. National Cancer Center. Cancer facts and figures 2009. 2009. Seoul: Ministry of Health and Welfare; p. 2-28 (Korean)
- 17. Obuchowski NA, McClish DK. Sample size determination for diagnostic accuracy studies involving binormal ROC curve indices. Stat Med 1997;16(13):1529-1542. 9249923ArticlePubMed
- 18. Atherly A, Fink AS, Campbell DC, Mentzer RM Jr, Henderson W, Khuri S, et al. Evaluating alternative risk-adjustment strategies for surgery. Am J Surg 2004;188(5):566-570. 15546571ArticlePubMed
- 19. Tourangeau AE, Tu JV. Developing risk-adjusted 30-day hospital mortality rates. Res Nurs Health 2003;26(6):483-496. 14689464ArticlePubMed
- 20. Tekkis PP, Poloniecki JD, Thompson MR, Stamatakis JD. Operative mortality in colorectal cancer: prospective national study. BMJ 2003;327(7425):1196-1201. 14630754ArticlePubMedPMC
- 21. Aylin P, Bottle A, Majeed A. Use of administrative data or clinical databases as predictors of risk of death in hospital: comparison of models. BMJ 2007;334(7602):1044. 17452389ArticlePubMedPMC
- 22. Mehrkhani F, Nasiri S, Donboli K, Meysamie A, Hedayat A. Prognostic factors in survival of colorectal cancer patients after surgery. Colorectal Dis 2009;11(2):157-161. 18462239ArticlePubMed
- 23. Liang H, Wang XN, Wang BG, Pan Y, Liu N, Wang DC, et al. Prognostic factors of young patients with colon cancer after surgery. World J Gastroenterol 2006;12(9):1458-1462. 16552821ArticlePubMedPMC
- 24. Tekkis PP, Prytherch DR, Kocher HM, Senapati A, Poloniecki JD, Stamatakis JD, et al. Development of a dedicated risk-adjustment scoring system for colorectal surgery (colorectal POSSUM). Br J Surg 2004;91(9):1174-1182. 15449270ArticlePubMed
- 25. Rabeneck L, Souchek J, El-Serag HB. Survival of colorectal cancer patients hospitalized in the Veterans Affairs Health Care System. Am J Gastroenterol 2003;98(5):1186-1192. 12809847ArticlePubMed
- 26. Fazio VW, Tekkis PP, Remzi F, Lavery IC. Assessment of operative risk in colorectal cancer surgery: the Cleveland Clinic Foundation colorectal cancer model. Dis Colon Rectum 2004;47(12):2015-2024. 15657649ArticlePubMed
- 27. Nan KJ, Qin HX, Yang G. Prognostic factors in 165 elderly colorectal cancer patients. World J Gastroenterol 2003;9(10):2207-2210. 14562379ArticlePubMedPMC
- 28. Longo WE, Virgo KS, Johnson FE, Oprian CA, Vernava AM, Wade TP, et al. Risk factors for morbidity and mortality after colectomy for colon cancer. Dis Colon Rectum 2000;43(1):83-91. 10813129ArticlePubMed
- 29. Compton CC, Fielding LP, Burgart LJ, Conley B, Cooper HS, Hamilton SR, et al. Prognostic factors in colorectal cancer. College of American Pathologists Consensus Statement 1999. Arch Pathol Lab Med 2000;124(7):979-994. 10888773ArticlePubMed
- 30. Hadorn DC, Keeler EB, Rogers WH, Brook RH. Assessing the performance of mortality prediction models. 1993. Santa Monica: RAND; p. 1-32
- 31. Harrell FE Jr, Lee KL, Mark DB. Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat Med 1996;15(4):361-387. 8668867ArticlePubMed
- 32. Johnson RW. An introduction to the bootstrap. Teach Stat 2001;23(2):49-54Article
- 33. Iezzoni LI. Risk adjustment for measuring health care outcomes. 2003. 3rd ed. Chicago: Health Administration Press; p. 195-300
- 34. Hanley JA, McNeil BJ. A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology 1983;148(3):839-843. 6878708ArticlePubMed
- 35. Steyerberg EW, Eijkemans MJ, Harrell FE Jr, Habbema JD. Prognostic modelling with logistic regression analysis: a comparison of selection and estimation methods in small data sets. Stat Med 2000;19(8):1059-1079. 10790680ArticlePubMed
- 36. Bilimoria KY, Bentrem DJ, Feinglass JM, Stewart AK, Winchester DP, Talamonti MS, et al. Directing surgical quality improvement initiatives: comparison of perioperative mortality and long-term survival for cancer surgery. J Clin Oncol 2008;26(28):4626-4633. 18574159ArticlePubMed
- 37. Al-Homoud S, Purkayastha S, Aziz O, Smith JJ, Thompson MD, Darzi AW, et al. Evaluating operative risk in colorectal cancer surgery: ASA and POSSUM-based predictive models. Surg Oncol 2004;13(2-3):83-92. 15572090ArticlePubMed
- 38. Tekkis PP, Kinsman R, Thompson MR, Stamatakis JD. Association of Coloproctology of Great Britain, Ireland. The Association of Coloproctology of Great Britain and Ireland study of large bowel obstruction caused by colorectal cancer. Ann Surg 2004;240(1):76-81. 15213621ArticlePubMedPMC
REFERENCES
| Variables | Survival n (%) | Death n (%) | p-value1 | Variables | Survival n (%) | Death n (%) | p-value1 | ||
|---|---|---|---|---|---|---|---|---|---|
| Sex | Male (n = 408) | 393 (96.3) | 15 (3.7) | 0.792 | LN dissection | No (n = 34) | 30 (88.2) | 4 (11.8) | 0.03 |
| Female (n = 244) | 236 (96.7) | 8 (3.3) | Yes (n = 618) | 599 (96.9) | 19 (3.1) | ||||
| Age (y) | <50 (n = 80) | 79 (98.8) | 1 (1.2) | 0.01 | Past surgery history | No (n = 616) | 595 (96.6) | 21 (3.4) | 0.37 |
| 50-59 (n = 121) | 119 (98.4) | 2 (1.6) | Yes (n = 36) | 34 (94.4) | 2 (5.6) | ||||
| 60-69 (n=208) | 203 (97.6) | 5 (2.4) | Emergency surgery | No (n = 596) | 584 (98.0) | 12 (2.0) | <0.01 | ||
| ≥70 (n=243) | 228 (93.8) | 15 (6.1) | Yes (n = 56) | 45 (80.4) | 11 (19.6) | ||||
| Health insurance | Medicaid (n = 41) | 40 (97.6) | 1 (2.4) | 1.00 | TNM staging | I (n = 114) | 110 (96.5) | 4 (3.5) | <0.012 |
| National health insurance (n=611) | 589 (96.4) | 22 (3.6) | II (n = 174) | 172 (98.9) | 2 (1.2) | ||||
| Arrhythmia | No (n = 568) | 546 (96.1) | 22 (3.9 ) | 0.34 | III (n = 207) | 201 (97.1) | 6 (2.9) | ||
| Yes (n = 84) | 83 (98.8) | 1 (1.2) | IV (n = 74) | 72 (97.3) | 2 (2.7) | ||||
| Other cardiac arrhythmia | No (n = 638) | 618 (96.9) | 20 (3.1) | 0.01 | Unknown (n = 83) | 74 (89.2) | 9 (10.8) | ||
| Yes (n = 14) | 11 (78.6) | 3 (21.4) | Body mass index (kg/m2) | <18 (n = 48) | 48 (90.6) | 5 (9.4) | 0.102 | ||
| Hypertension | No (n = 351) | 342 (97.4) | 9 (2.6) | 0.202 | 18-25 (n = 430) | 414 (96.3) | 16 (3.7) | ||
| Yes (n = 301) | 287 (95.4) | 14 (4.7) | 25-30 (n = 153) | 151 (98.7) | 2 (1.3) | ||||
| Diabetes | No (n = 437) | 422 (96.6) | 15 (3.4) | 0.832 | ≥30 (n = 16) | 16 (100.0) | 0 (0.0) | ||
| Yes (n = 215) | 207 (96.3) | 8 (3.7) | Unknown (n = 5) | 4 (80.0) | 1 (20.0) | ||||
| Secondary cancer | No (n = 606) | 588 (97.0) | 18 (3.0) | 0.02 | Albumin (mg/dL) | <3 (n = 78) | 74 (94.9) | 4 (5.1) | 0.71 |
| Yes (n = 46) | 41 (89.1) | 5 (10.9) | ≥3 (n = 573) | 554 (96.7) | 19 (3.3) | ||||
| Liver disease | No (n = 457) | 444 (97.2) | 13 (2.8) | 0.172 | Unknown (n = 1) | 1 (100.0) | 0 (0.0) | ||
| Yes (n = 195) | 185 (94.9) | 10 (5.1) | ASA score | <3 (n = 577) | 566 (98.1) | 11 (1.9) | <0.01 | ||
| Admission through emergency room | No (n = 543) | 529 (97.4) | 14 (2.6) | 0.01 | ≥3 (n = 75) | 63 (84.0) | 12 (16.0) | ||
| Yes (n = 109) | 100 (91.7) | 9 (8.3) | Perforation of colon | No (n = 618) | 601 (97.3) | 17 (2.8) | <0.01 | ||
| Yes (n = 34) | 28 (82.4) | 6 (17.7) | |||||||
| Associated surgery | No (n = 574) | 554 (96.5) | 20 (3.5) | 0.75 | Obstruction of colon | No (n = 518) | 507 (97.9) | 11 (2.1) | <0.01 |
| Yes (n = 78) | 75 (96.2) | 3 (3.9) | Yes (n = 134) | 122 (91.0) | 12 (9.0) |
| Variables | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | |
|---|---|---|---|---|---|---|
| Age (y) | <50 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 50-59 | 1.785 | 1.743 | 1.643 | 1.774 | 1.534 | |
| 60-69 | 2.979 | 1.593 | 1.802 | 2.79 | 2.373 | |
| ≥70 | 8.236 | 7.184 | 7.595 | 7.705 | 5.267 | |
| Sex | Male | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Female | 0.813 | 0.700 | 0.589 | 0.829 | 0.719 | |
| Health insurance | Medicaid | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| National health insurance | 5.204 | 6.736 | 3.174 | 4.488 | 4.238 | |
| Diabetes | 0.762 | 0.677 | 0.617 | 0.602 | 0.516 | |
| Hypertension | 0.942 | 0.865 | 1.273 | 0.998 | 1.470 | |
| Liver disease | 2.912* | 3.342* | 5.019* | 4.297* | 1.550 | |
| Other cardiac arrhythmia | 12.76* | 29.099* | 37.411* | 13.481 | 5.197* | |
| Secondary cancer | 4.857* | 5.761* | 3.371 | 4.480* | 2.912 | |
| Admission through emergency room | 3.817* | 3.554* | - | - | - | |
| LN dissection | 0.224 | 0.315 | 0.294 | 1.646 | 0.241 | |
| Associated surgery | 1.425 | 1.403 | 1.125 | 0.165 | 0.883 | |
| Emergency surgery | 3.475 | 2.503 | ||||
| Past surgery history | 0.271 | 0.293 | ||||
| TNM staging | I | 1.000 | 1.000 | 1.000 | ||
| II | 0.181 | 0.136 | 0.284 | |||
| III | 0.670 | 0.726 | 0.551 | |||
| IV | 0.593 | 0.298 | 0.270 | |||
| Unknown | 2.896 | 3.334 | 2.125 | |||
| Perforation of colon | 5.932* | 5.301* | ||||
| Obstruction of colon | 3.564 | 1.672 | ||||
| Body mass index (kg/m2) | 18.5-25 | 1.000 | 1.000 | |||
| <18.5 | 1.693 | 1.651 | ||||
| ≥25 | 0.194 | 0.242 | ||||
| Unknown | 2.477 | 4.277 | ||||
| ASA score | <3 | 1.000 | 1.000 | |||
| ≥3 | 11.23* | 7.436* | ||||
| Serum albumin (mg/dL) | <3 | 1.000 | 1.000 | |||
| ≥3 | 1.068 | 1.479 | ||||
| Unknown | <0.001 | <0.001 |
Figure & Data
References
Citations

- Estimating postoperative mortality in colorectal surgery- a systematic review of risk prediction models
Alexios Dosis, Jack Helliwell, Aron Syversen, Jim Tiernan, Zhiqiang Zhang, David Jayne
International Journal of Colorectal Disease.2023;[Epub] CrossRef - Modified Tumor Budding as a Better Predictor of Lymph Node Metastasis in Early Gastric Cancer: Possible Real-World Applications
Kwangil Yim, Won Mo Jang, Sung Hak Lee
Cancers.2021; 13(14): 3405. CrossRef - Investigación epidemiológica en cáncer colorrectal: perspectiva, prospectiva y retos bajo la óptica de explotación del Big-Data
J.M. García Torrecillas, M. Ferrer Márquez, Á. Reina Duarte, F. Rubio-Gil
SEMERGEN - Medicina de Familia.2016; 42(8): 509. CrossRef - Variation between Hospitals with Regard to Diagnostic Practice, Coding Accuracy, and Case-Mix. A Retrospective Validation Study of Administrative Data versus Medical Records for Estimating 30-Day Mortality after Hip Fracture
Jon Helgeland, Doris Tove Kristoffersen, Katrine Damgaard Skyrud, Anja Schou Lindman, Alanna M Chamberlain
PLOS ONE.2016; 11(5): e0156075. CrossRef - Model for risk adjustment of postoperative mortality in patients with colorectal cancer
K Walker, P J Finan, J H van der Meulen
British Journal of Surgery.2015; 102(3): 269. CrossRef - Problems With Public Reporting of Cancer Quality Outcomes Data
Paul Goldberg, Rena M. Conti
Journal of Oncology Practice.2014; 10(3): 215. CrossRef
 KSPM
KSPM

 PubReader
PubReader ePub Link
ePub Link Cite
Cite